المتسلسلات الهندسية اللانهائية - رياضيات2-2 - ثاني ثانوي

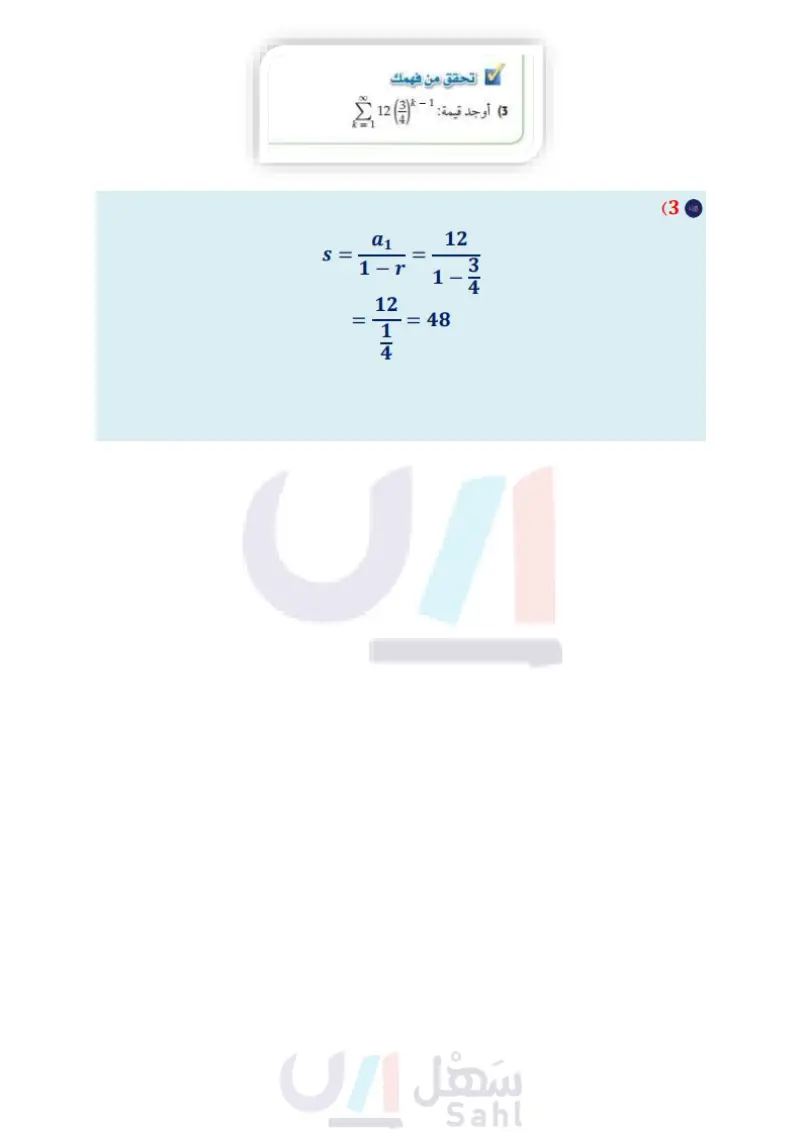
6-4 فيما سبق متسلسلة هندسية المتسلسلات الهندسية اللانهائية Infinite Geometric Series الماذا؟ أنشأ رسام لوحة فنية هندسية مستعملا المثلثات المتطابقة الأضلاع فقط كما في الشكل درست إيجاد مجموع حدود المجاور، إذا كان طول ضلع المثلث الخارجي 15in ، والمثلث الذي يليه من الداخل ينتج عن منتهية (الدرس (63) توصيل منتصفات أضلاع المثلث الخارجي، إذا استمر في عملية رسم المثلثات الداخلية بهذا النمط، فكم سيكون مجموع محيطات كل المثلثات المكوّنة للشكل ؟ يمكن الإجابة عن مثل هذه الأسئلة، بدراسة المتسلسلات الهندسية غير المنتهية (اللانهائية). وا الان . أجد مجموع حدود متسلسلة هندسية غير منتهية لانهائية). أكتب الكسر العشري المتسلسلة الهندسية اللانهائية المتسلسلة الهندسية التي لها عدد لا نهائي www.ien.edu.sa -15 in من الحدود تُسمى المتسلسلة الهندسية اللانهائية، والمجموع الجزئي لمتسلسلة لا نهائية (S) هو مجموع عدد محدد (11) من حدودها، وليس مجموع كل حدودها، والمتسلسلة الهندسية اللانهائية تكون متقاربة عندما تقترب الدوري في صورة كسر مجاميعها الجزئية (5) من عدد ثابت كلما زادت قيمة ،11، وعندما لا تقترب هذه المجاميع من عدد ثابت مع زيادة قيمة 11 فإن المتسلسلة الهندسية اللانهائية تكون متباعدة. اعتيادي. المفردات: المتسلسلة الهندسية اللانهائية infinite geometric series المجموع الجزئي لمتسلسلة لا نهائية partial sum المتسلسلة المتقاربة أوجدت في الدرس السابق مجموع أول 1 حدا من متسلسلة هندسية لا نهائية، ويمكنك أيضًا إيجاد مجموع كل حدودها. ففي فقرة "لماذا؟ أعلاه تجد أن مجموع محيطات المثلثات المكوّنة للشكل تُعطى بالمتسلسلة اللانهائية ... + 11.25 + 22.5 + 45 ، وكلما زاد عدد حدودها، فإن مجموعها يقترب من 90in (وهو المجموع الفعلي لها عندما يزداد عدد حدودها إلى مالا نهاية. والشكل أدناه يظهر التمثيل البياني للمجموع 5 ، حيث 10 = n = 1 مفهوم أساسي المتسلسلات الهندسية المتقاربة والمتباعدة أضف إلى مطويتك المتسلسلات الهندسية المتباعدة convergent series divergent series المتسلسلة المتباعدة مالانهاية infinity التعبير اللفظي: إذا كانت النسبة المشتركة التعبير اللفظي إذا كانت النسبة المشتركة المتسلسلات الهندسية المتقاربة (الأساس) 1 > || : فإن المجموع الجزئي يقترب من عدد ثابت مثال (الأساس) 1 : فإن المجموع الجزئي لا يقترب من عدد ثابت. 1 1 1 +... + + 4 16 8 إرشادات للدراسة المجاميع الجزئية يمكن توضيح التمثيل البياني للمجاميع الجزئية للمتسلسلة الواردة في فقرة "لماذا؟ " بإنشاء الجدول التالي: المجموع عدد الجزئي 5 الحدود 1 مثال: 4522.5+ 11.25 + ... المجموع الجزئي (5) 90 80 70 60 50 40 30 20 10 0 1 2 3 4 5 6 7 8 9 " عدد الحدود (1) المجموع الجزئي (5) 1.8 1.6 1.4 1.2 1.0 0.8 0.6 0.4 0.2 0 1 2 3 4 5 6 7 8 9 n عدد الحدود (1) مثال 1 المتسلسلات المتقاربة والمتسلسلات المتباعدة 1 حدد أي المتسلسلتين الهندسيتين الآتيتين متقاربة، وأيهما متباعدة: 5 = 45 S₂ =45+22.5 2 54 +36 +24 + ... (a =67.5 $3 45+22.5+ 3 11.25=78.75 أوجد قيمة r 36 = = r ، وبما أن 1 > > 1- فإن المتسلسلة متقاربة. وزارة التعليم الدرس 4- المتسلسلات الهندسية اللانهائية 145 2024-1446

إرشادات للدراسة القيمة المطلقة تذكر أن 1 || تعني -1<r<1i أما 1 2 | 1 | فتعني أن 1 r أو 1- 7 8+12+18+... (b 1.5 = 1 = r ، وبما أن 1 < 1.5، فإن المتسلسلة متباعدة. تحقق من فهمك 2+3+4.5+ ... (1A 100+50+25+... (1B إذا كانت 1 > ۱۲ ، فإن قيمة "" تقترب من الصفر كلما زادت قيمة 1 ، ولذلك فإن المجاميع الجزئية للمتسلسلة إرشادات للدراسة التقارب والتباعد تتقارب المتسلسلة الهندسية اللانهائية عندما تكون القيمة المطلقة لأي حد فيها أقل من القيمة المطلقة للحد السابق له وتكون المتسلسلة الحسابية اللانهائية متباعدة دائما. 146 الهندسية اللانهائية تقترب من مفهوم أساسي a1 r a₁ (1-0) 1-r أضف إلى مطويتك n S. 5 10 15 1364 1398100 1431655764 مجموع المتسلسلة الهندسية اللانهائية المتقاربة مجموع حدود المتسلسلة الهندسية اللانهائية المتقاربة يُرمز له بالرمز S حيث 1 > || ويُعطى بالصيغة 1 = 5 ستشتق صحة هذه الصيغة في السؤال (36) وعندما تكون المتسلسلة الهندسية اللانهائية متباعدة، (1 )، فإنه لا يوجد مجموع لحدود المتسلسلة؛ لأن قيمة "" تزداد بلا حدود مع زيادة " . والجدول المجاور يوضح المجاميع الجزئية للمتسلسلة الهندسية المتباعدة ... + 64 +16+ 4 ، حيث إنه كلما زادت قيمة ، فإن تزداد بسرعة كبيرة جدًّا. مثال 2 مجموع المتسلسلة الهندسية اللانهائية أوجد مجموع حدود كل من المتسلسلتين الهندسيتين الآتيتين إن وجد: + + + ... (a الخطوة 1: أوجد قيمة " للتأكد من وجود المجموع من عدمه. = : = ۲ اقسم الحد على الحد السابق له مباشرة بما أن 1 > ، فإن للمتسلسلة مجموعا. الخطوة 2 استعمل المعادلة لإيجاد المجموع. 6+9+13.5+ 20.25 + ... (b صيغة المجموع بسط 1.5 = 2 = r؛ وبما أن 1 1.5 ، فإن المتسلسلة متباعدة وليس لها مجموع. تحقق من فهمك 16+20+25+... (2B 4 - 2 + 1 - 0.5 + ... (2 الفصل 6 المتتابعات والمتسلسلات وزارة التعليم Ministry of Education 2024-1446

إرشادات للدراسة رمز المجموع للمتسلسلة الهندسية اللانهائية atar+ar +...+ay pk-1+... - Σα k=1 يمكنك استعمال رمز المجموع لكتابة المتسلسلات الهندسية اللانهائية، وهي التي تستمر حدودها إلى ما لانهاية؛ أي أنها تستمر دون توقف، ويُستعمل الرمز فوق رمز المجموع للدلالة على ذلك. رمز المجموع والمتسلسلة اللانهائية مثال 3 أوجد قيمة: 1 - (3) 18 k=1 18 18 = = 90 صيغة المجموع = = 1 = 4 ، ثم بسط بسط تحقق من فهمك 3) أوجد قيمة: 1 - 12 الكسور الدورية : الكسر العشري الدوري هو مجموع متسلسلة هندسية لانهائية. فعلى سبيل المثال ... + 0.000045 + 0.0045 + 0.45 = ...0.454545 = 0.45 . ويمكن استعمال صيغة مجموع المتسلسلة الهندسية اللانهائية لتحويل هذا الكسر العشري الدوري إلى كسر اعتيادي. مثال 4 تحويل الكسر العشري الدوري إلى كسر اعتيادي إرشادات للدراسة الكسور الدورية الكسر العشري الدوري هو عدد نسبي، ويمكن كتابته في صورة كسر اعتيادي. اكتب الكسر العشري الدوري 0.63 في صورة كسر اعتيادي. الطريقة 1: باستعمال مجموع متسلسلة هندسية لانهائية 63 0.63 0.63 + 0.0063+... + 100 63 + ... 10000 a صيغة المجموع 63 63 1 100 a₁ = 100 100 1- 100 63 7 بسط 99 11 إرشادات لحل المسألة اختيار الأسلوب الأفضل للحساب في كثير من الأحيان يمكن حل المسألة بأكثر من طريقة ولذلك استعمل الطريقة التي تفضلها. الطريقة 2 : باستعمال الخواص الجبرية تحقق من فهمك x = 0.63 x = 0.636363... 100x 63.636363... 99x = 63 x= 63 99 7 11 افترض 0.63 = x اكتب في صورة كسر عشري دوري اضرب كلا الطرفين في 100 اطرح x من 100x و 0.63 من 63.63 اقسم الطرفين على 99 4) اكتب الكسر العشري الدوري 0.21 في صورة كسر اعتيادي. وزارة التعليم الدرس 4-6 المتسلسلات الهندسية اللانهائية 147 2024-1446

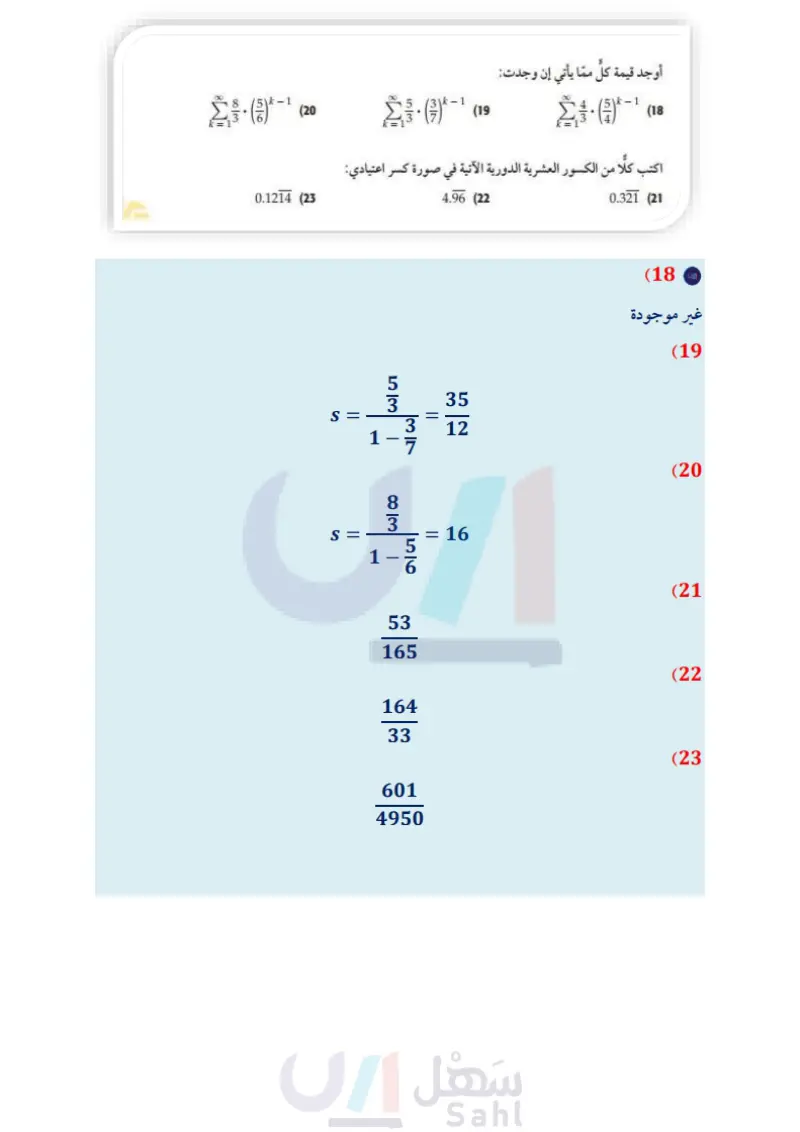
وزارة التعليم Ministry of Education 2024-1446 تأكد مثال 1 حدد أي المتسلسلتين الهندسيتين الآتيتين متقاربة، وأيهما متباعدة: 16 84 ... (1 1+1+1+... (2 مثال 2 أوجد مجموع حدود كل من المتسلسلتين الهندسيتين الآتيتين إن وجد: 440+220 + 110+... (3 مثال 3 أوجد قيمة كل مما يأتي إن وجدت: 5-4-1 (5 k=1 9 + +... (4) 4 16 8 (-2) (0.5)-1 (6 k=1 مثال 4 اكتب كلا من الكسرين العشريين الدوريين الآتيين في صورة كسر اعتيادي: 0.642 (8 0.35 (7 تدرب وحل المسائل مثال 1 حدد أي المتسلسلات الهندسية الآتية متقاربة، وأيها متباعدة: (10 0.008+0.08+0.8+... (12 6 ft 2163189+... (9 0.1+0.01+0.001 +... (11 مثال 2 أوجد مجموع حدود كل من المتسلسلات الهندسية الآتية إن وجد: -3 4.2 5.88 (14) 3240+ 50+... (16 (20 0.1214 (23 18+ 21.6 25.92+... (13 3 + 3 + 3 + ... (15 5 (17) أراجيح انطلق سعيد من نقطة البداية الموضحة في الشكل المجاور، تاركًا نفسه بعد ذلك من دون دفع منه، فبدأت مسافة التأرجح تتناقص بمقدار %10% في كل تأرجح، أوجد المسافة الكلية التي يكون سعيد قد قطعها عندما تتوقف الأرجوحة تماما. مثال 3 أوجد قيمة كل مما يأتي إن وجدت: 2018 k - 1 (18 -1 (19 مثال 4 اكتب كلا من الكسور العشرية الدورية الآتية في صورة كسر اعتيادي: 4.96 (22 0.321 (21 الفصل 6 المتتابعات والمتسلسلات 148

(24) بطاريات قابلة للشحن : أعلنت إحدى شركات صناعة البطاريات القابلة للشحن، عن بطارية تشحن بفاعلية نسبتها %99.9% من الفاعلية السابقة بعد كل مرة يتم فيها شحن البطارية. إذا كانت شحنتها في البداية تكفي للعمل 8 ساعات، فما أكبر عدد من الساعات يمكن أن تُستعمل فيه البطارية؟ أوجد مجموع حدود كل من المتسلسلات الآتية إن وجد: 1 + 3 + 3 + +... (25 21 16 7 +... (27 -16-1 -1+... (26 الربط بالحياة استعملت البطاريات في العالم منذ أكثر من 100 عام، وهي مطلوبة الآن أكثر من أي وقت مضى، ولذلك فإن أكثر من 3 بلايين بطارية تتلف في كل عام. ويمكن استعمال بطارية واحدة من البطاريات القابلة للشحن بدلا من 100 بطارية عادية. إرشادات للدراسة أساس المتسلسلة في السؤال 32 تنقص المسافة التي يقطعها (28) تمثيلات متعددة ستحتاج في هذه المسألة إلى بطاقة مربعة الشكل طول ضلعها لا يقل عن 8 بوصات. a حسيا : افترض أن مساحة البطاقة تُمثل وحدة مربعة. قُصّ البطاقة نصفين، خذ أحدهما واعتبره الحد الأول، ثم قُصَّ النصف الآخر نصفين واعتبر أحدهما الحدّ الثاني. استمر في هذه العملية، واكتب المتسلسلة اللانهائية، التي تعبر عن الأجزاء لديك. 6 عدديا : إذا أمكن تقسيم البطاقة بهذه الطريقة إلى مالانهاية، فما مجموع المتسلسلة التي أوجدتها في الفرع a؟ ما العلاقة بين مجموع المتسلسلة ومساحة البطاقة الأصلية؟ 29) فيزياء في تجربة فيزيائية دحرجت كرة من الفولاذ على مسار أفقي، وتركت لتتدحرج تلقائيا، فإذا قطعت الكرة في الدقيقة الأولى 120ft ، ثم بدأت تقطع في كل دقيقة 40% فقط من المسافة التي قطعتها في الدقيقة السابقة، فما المسافة الكلية التي : تقطعها الكرة حتى تقف؟ (30) بندول: يقطع بندول مسافة 12cm في الاهتزازة الأولى، وبعد ذلك يقطع %95% من الاهتزازة السابقة، ويستمر على هذا المنوال أوجد المسافة الكلية التي يقطعها البندول حتى يتوقف عن الحركة. 31) كرات أسقطت كرة مطاطية من ارتفاع 30ft، فكانت ترتد في كل مرة مسافة تعادل %95 من المسافة السابقة. إذا استمرت الكرة في الحركة على هذا المنوال، فأوجد المسافة التي تقطعها حتى تقف. (32) متحف العلوم : يُتيح أحد المعارض في متحف للعلوم الفرصة للزوار لتجربة حركة الأجسام على زنبرك. فإذا قام أحد الزوار بسحب جسم معلّق بزنبرك إلى أسفل، ثم تركه ليقطع مسافة 1.2 إلى أعلى قبل أن يُغير اتجاه حركته، وفي كل مرة يغيّر الجسم اتجاه حركته تنقص المسافة التي يقطعها بمقدار 20 بالمقارنة مع المسافة في الاتجاه الآخر السابق، فأوجد المسافة الكلية التي يقطعها الجسم. الجسم المعلق بالزنبرك اربط بين كل شكل والوصف المناسب له : 20%، أي أن المسافة التي يقطعها الجسم تمثل 80% من المسافة السابقة لها قبل أن يغير اتجاه حركته. (33 عدد الحدود (1) a متسلسلة هندسية متقاربة. المجموع الجزئي (5) S (34 عدد الحدود (1) متسلسلة هندسية متباعدة. متسلسلة حسابية متقاربة. d متسلسلة حسابية متباعدة. وزارة التعليم الدرس 4-6 المتسلسلات الهندسية اللانهائية 149 2024-1446

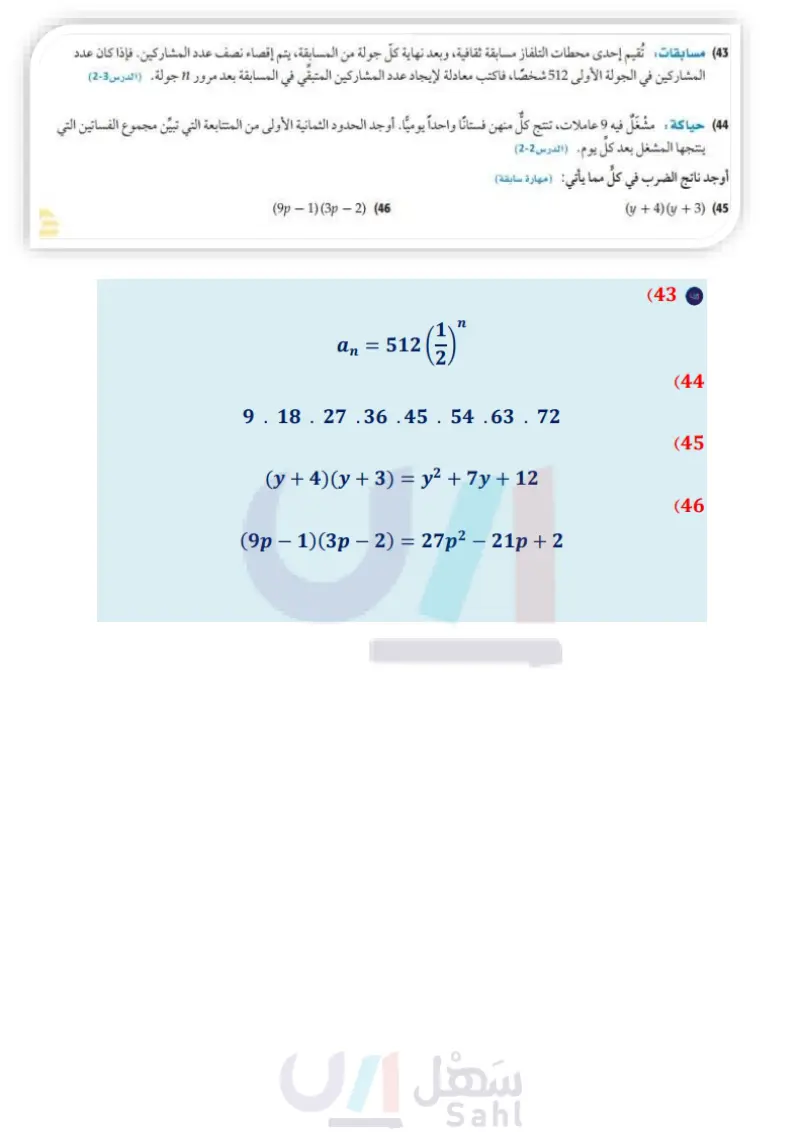
تدريب على اختبار مسائل مهارات التفكير العليا 35) اكتشف الخطأ: طلب إلى كلِّ من علي وأحمد أن يجد مجموع المتسلسلة ... - 1 + 1 – 1 فكانت إجابتاهما كما يأتي. فهل إجابة أي منهما صحيحة؟ وضح تبريرك. علي المجموع صفر، لأن مجموع كل زوج من الحدود في المتسلسلة هو الصفر. أحمد لا يمكن إيجاد المجموع، لأن 21 || ، والمتسلسلة متباعدة. (36) صيغ اشتق معادلة مجموع متسلسلة هندسية لا نهائية. 37) تحد ما قيم التي يمكن عندها إيجاد مجموع المتسلسلة ... + 8103 + 2762 + 96 + 3 ؟ 38 تبرير متى يكون للمتسلسلة الهندسية مجموع ، ومتى لا يكون؟ وضح تبريرك. (39) مسألة مفتوحة : اكتب المتسلسلة ... - 12 - 6 - 3 باستعمال رمز المجموع وبطريقتين مختلفتين. 40) اكتب وضّح لماذا تكون المتسلسلة الحسابية متباعدة دائمًا. 41) مجموع المتسلسلة الهندسية اللانهائية التي حدها الأول 27 ، (42) هندسة ضُرب نصف قطر كرة كبيرة في العدد 3 وأساسها و هو : للحصول على كرة أصغر ما حجم الكرة الصغيرة بالمقارنة مع حجم الكرة الكبيرة؟ 81 A 65 B 34 C 18 D مراجعة تراكمية A 9 B C D حجم الكبيرة الكبيرة حجم حجم الكبيرة حجم الكبيرة (43) مسابقات تقيم إحدى محطات التلفاز مسابقة ثقافية، وبعد نهاية كل جولة من المسابقة، يتم إقصاء نصف عدد المشاركين. فإذا كان عدد المشاركين في الجولة الأولى 512 شخصًا، فاكتب معادلة لإيجاد عدد المشاركين المتبقي في المسابقة بعد مرور 11 جولة (الدرس 3-6) 44) حياكة : مشغل فيه 9 عاملات، تنتج كلّ منهن فستانًا واحداً يومياً. أوجد الحدود الثمانية الأولى من المتابعة التي تبين مجموع الفساتين التي ينتجها المشغل بعد كل يوم. (الدرس 2-6) أوجد ناتج الضرب في كل مما يأتي: (مهارة سابقة) (y+4)(y+3) (45 الفصل 6 المتتابعات والمتسلسلات 150 (9p 1)(3p 2) (46 وزارة التعليم Ministry of Education 2024-1446